Some utilities

ecolopy_dev.utils.generate_random_neutral_abundance(model_name, size, **kwargs)

Parameters:

• model_name – model name (ewens, etienne, lognorm)
• size – size of the community (J), if log-normal distribution size should be equal to number of species (S)

Returns:

random neutral distribution of abundance

other args should be of kind theta, I, m

Example:

import ecolopy_dev
ecolopy.generate_random_neutral_abundance('ewens', 100, theta=12, I=12)

ecolopy_dev.utils.shannon_entropy(abund, inds)

computes Shannon entropy (H) for a given abundance table and number of individuals.

Parameters:abund – distribution of abundances as list Returns:Shannon entropy

ecolopy_dev.utils.draw_contour_likelihood(abd, model=None, theta_range=None, m_range=None, num_dots=100, local_optima=True, write_lnl=False)

Draw contour plot of the log likelihood of a given abundance to fit Etienne model.

Parameters:

• abd – Community object
• model (None) – model name, if None current model is used
• theta_range (None) – minimum and maximum value of theta as list. If None, goes from 1 to number of species (S)
• m_range (None) – minimum and maximum value of m as list. If None, goes from 0 to 1
• num_dots (100) – Number of dots to paint
• local_optima (True) – display all local optima founds as white cross
• write_lnl (False) – allow to write likelihood values manually by left click on the contour plot.

ecolopy_dev.utils.draw_shannon_distrib(neut_h, obs_h, outfile=None, filetype=None, size=(15, 15))

draws distribution of Shannon values for random neutral

Parameters:

• neut_h – list of Shannon entropies corresponding to simulation under neutral model
• obs_h – Shannon entropy of observed distribution of abundance
• outfile (None) – path were image will be saved, if none, plot will be shown using matplotlib GUI
• filetype (None) – pdf or png
• size ((15,15)) – size in inches of the drawing

ecolopy_dev.utils.fast_etienne_likelihood(mod, params, kda=None, kda_x=None)

same as Abundance inner function, but takes advantage of constant m value when varying only theta.

Parameters:

• abd – Abundance object
• params – list containing theta and m
• kda_x – precomputed list of exp(kda + ind*immig)

ecolopy_dev.utils.pre_get_stirlings(max_nm, needed, verbose=True)

takes advantage of recurrence function:

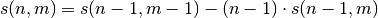
and as s(whatever, 0) = 0 :

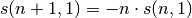
keep only needed stirling numbers (necessary for large communities)

Parameters:

• max_nm – max number of individuals in a species
• needed – list of individuals count in species in our dataset, needed in order to limit the number of stirling numbers kept in memory.
• verbose (True) – displays information about state.

ecolopy_dev.utils.mul_polyn(polyn_a, polyn_b)

computes the product of 2 polynomials, depending of the differences in length of the two polynomials, this function will call one of: * _mul_uneq_polyn: when length of polyn_a is >= length of polyn_b, will iterate over coefficient. * _mul_simil_polyn: in case both polynomials have equal length, will iterate over factors.

to test multiplication of pylnomials try equality of the two functions: mul_uneq_polyn(polyn_a, polyn_b, len_a, len_b) == _mul_simil_polyn(polyn_a, polyn_b, len_a, len_b)

Example:

from ecolopy_dev.utils import mul_polyn
# (2 + 3^x + 5x^2)  * (x)
mul_polyn([2,3,5], [0,1])
# will return: [mpfr('0.0'), mpfr('2.0'), mpfr('3.0'), mpfr('5.0')]
# that is: 0 + 2x + 3x^2 + 5x^3

Parameters:

• polyn_a – list of indices of polynomial
• polyn_b – list of indices of polynomial (e.g.: [1,3,5,0,2] for )

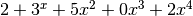Returns:

a list representing multiplication of the two polynomials

ecolopy_dev.utils.power_polyn(polyn_a, power)

ecolopy_dev.utils.table(out, spp=None)

data to contingency table any kind of data

Parameters:out – species abundance Returns:list of counts of individuals by species